• Ploss Valve
• Ploss Valve
• Ploss Valve Pic

(a)Identification. A switching valve (ploss) is a three-way valve located between a stethoscope placed over the heart, a blood pressure cuff, and an earpiece. The valve allows the user to eliminate one sound channel and listen only to a patient's heart or korotkoff (blood pressure) sounds through the other channel.

(b)Classification. Class I (general controls). The device is exempt from the premarket notification procedures in subpart E of part 807 of this chapter subject to the limitations in § 868.9. The device is also exempt from the current good manufacturing practice requirements of the quality system regulation in part 820 of this chapter, with the exception of § 820.180, with respect to general requirements concerning records, and § 820.198, with respect to complaint files.

Minor pressure and head loss in pipes, tubes and duct systems

Pressure loss in straight pipes or ducts are called the major, linear or friction loss. Pressure loss in components like valves, bends, tees and similar are called the minor, dynamic or local loss.

Minor loss can be significant compared to major loss. In fact - when a valve is closed or nearly closed - the minor loss is infinite. For an open valve the minor loss can often be neglected (typical for a full bore ball valve).

DossSutureless aortic valve replacement with the 3f Enable aortic bioprosthesis Ann Thorac Surg, 87 (2009), pp. 1914-1917 Article Download PDF View Record in Scopus Google Scholar. Pressure drop or head loss is proportional to the velocity in valves or fittings. For the most engineering practices it can be assumed that pressure drop or head loss due to flow of fluids in turbulent range through valves and fittings is proportional to square of velocity.

Minor Loss

The pressure drop or the minor loss in a component correlates to the dynamic pressure in the flow and can be expressed as

Δp_{minor_loss} = ξ p_d

= ξ ρ_f v² / 2 (1)

where

ξ = minor loss coefficient

p_d = dynamic pressure in fluid flow (Pa (N/m²), psf (lb/ft²))

Δp_{minor_loss} = minor pressure loss (Pa (N/m²), psf (lb/ft²))

ρ_f = density of fluid (kg/m³, slugs/ft³)

v = flow velocity (m/s, ft/s)

The minor loss can be expressed as head water column by dividing the dynamic pressure with the specific weight of water

Δh_{minor_loss,w} = (ξ ρ_f v² / 2) / γ_w

= (ξ ρ_f v² / 2) / (ρ_wg)

= ξ ρ_fv² / (2 ρ_wg) (2)

where

Δh_{minor_loss,w} = minor head loss as water column (m H2O, ft H2O)

γ_w = ρ_w g = specific weight of water or reference fluid (9807 N/m³, 62.4 lb_f/ft³)

g = acceleration of gravity (9.81 m/s², 32.174 ft/s²)

• 1 psf = 0.00694 psi (lb/in²)

Note! - in the equation above the head is related to water as the reference fluid. Another reference fluid can be used - like Mercury Hg - by replacing the density of water with the density of the reference fluid - check Velocity Pressure Head.

If the flowing fluid has the same density as the reference fluid - typical for a water flow - eq. (2) can simplified to

Δh_{minor_loss} = ξ v² / (2 g) (2b)

where

Δh_{minor_loss} = minor head loss (column of flowing fluid) (m fluid column, ft fluid column)

Minor Loss Coefficient

The minor loss coefficient - ξ - values ranges from 0 and upwards. For ξ = 0 the minor loss is zero and for ξ = 1 the minor loss is equal to the dynamic pressure or head. The minor loss coefficient can also be greater than 1 for some components.

The minor loss coefficient can be expressed by rearranging (1) to

ξ = 2 Δp_{minor_loss} / (ρ_f v²) (3)

The minor loss coefficient can alternatively be expressed by rearranging (2) to

Ploss Valve

ξ = 2 ρ_wg Δh_{minor_loss,w} / (ρ_fv²) (4)

The dynamic loss in components depends primarily on the geometrical construction of the component and the impact the construction has on the fluid flow due to change in velocity and cross flow fluid accelerations.

The fluid properties - in general expressed with the Reynolds number - also impacts the minor loss.

Minor loss information about components are given in dimensionless form based on experiments.

Equivalent Length

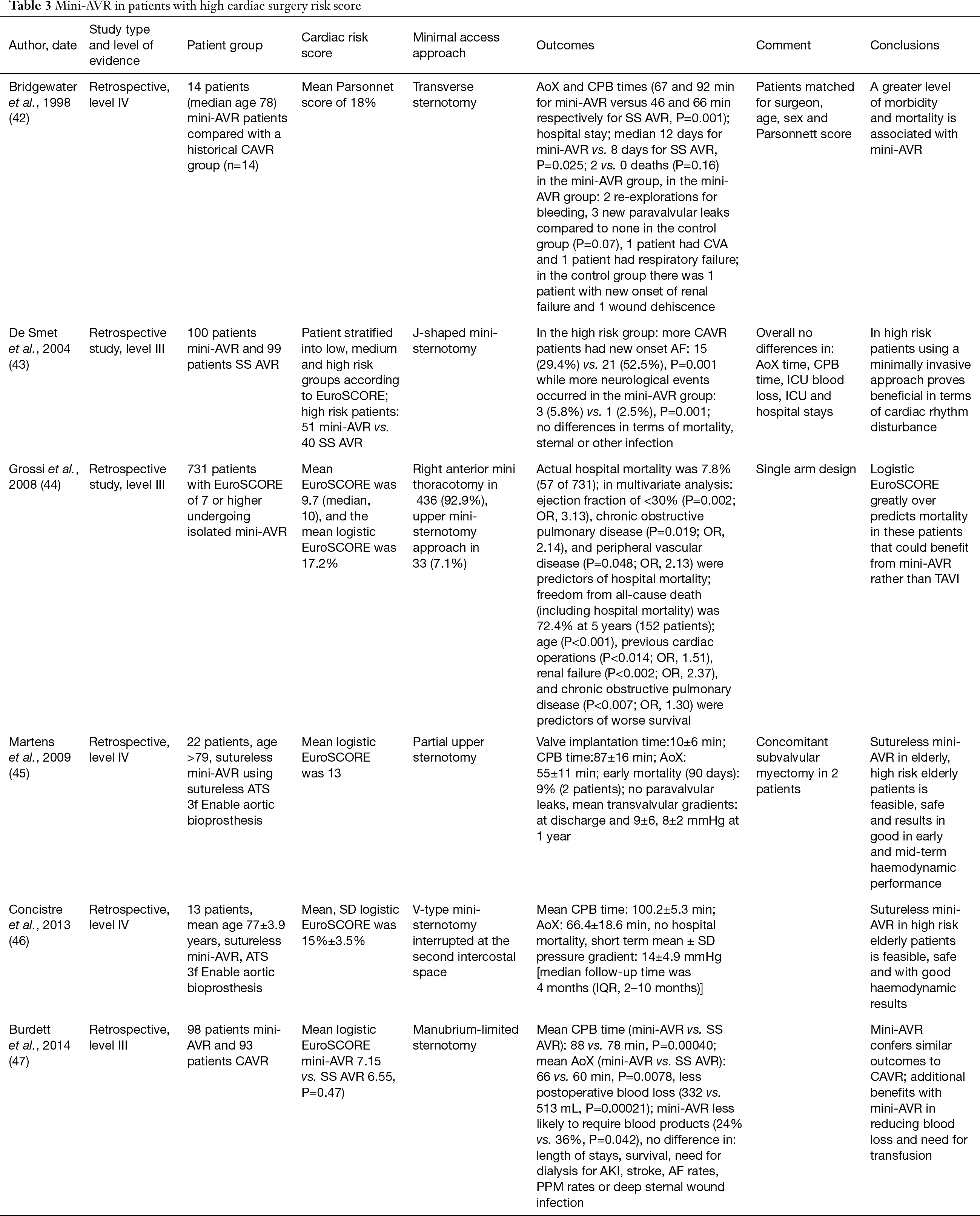
The dynamic minor loss in a component can be converted to an equivalent length of pipe or tube that would give the same major loss.

Major loss in a fluid flow can be expressed as

Δp_{major_loss} = λ (l / d_h) (ρ_f v² / 2) (5)

where

Δp_{major_loss} = major (friction) pressure loss in fluid flow (Pa (N/m²), psf (lb/ft²))

λ = Darcy-Weisbach friction coefficient

l = length of duct or pipe (m, ft)

v = velocity of fluid (m/s, ft/s)

d_h = hydraulic diameter (m, ft)

ρ_f = density of fluid (kg/m³, slugs/ft³)

If we want the minor loss to be equal to the major loss for a given equivalent length of pipe or duct - then

Δp_{minor_loss} = Δp_{major_loss, eq} (6)

or by combining (1) and (2)

ξ ρ_f v² / 2 = λ (l_eq / d_h) (ρ_f v² / 2) (6b)

where

Δp_{major_loss, eq}= equivalent major loss (Pa (N/m²), psf (lb/ft²))

l_eq = equivalent pipe length (m, ft)

(6b) can be reduced and rearranged to express equivalent length as

l_eq = ξ d_h / λ (7)

The total head loss in a pipe, tube or duct system, is the same as that produced in a straight pipe or duct whose length is equal to the pipes of the original systems - plus the sum of the equivalent lengths of all components in the system.

Example - Equivalent Length of Gate Valve

The equivalent length of a 50 mm gatevalve with loss coefficient0.26 when 1/4 closed located in a steel pipe with friction coefficient0.03 can be calculated with (7) as

l_eq = 0.26 (0.05 m) / 0.03

= 0.4 m

Related Topics

• Fluid Mechanics - The study of fluids - liquids and gases. Involves velocity, pressure, density and temperature as functions of space and time
• Fluid Flow and Pressure Loss - Pipe lines - fluid flow and pressure loss - water, sewer, steel pipes, pvc pipes, copper tubes and more

Related Documents

• Air Duct Components and Minor Dynamic Loss Coefficients - Minor loss - pressure or head loss - coefficients for air duct distribution systems components
• Air Ducts - Friction Loss Diagram - Major loss diagram for air ducts - SI units
• Air Ducts Minor Loss Coefficient Diagrams - Minor loss coefficient diagrams for air ductwork, bends, expansions, inlets and outlets - SI units
• Air Flow and Velocity due to Natural Draft - Air flow - volume and velocity - due to stack or flue effect caused by indoor hot and outdoor cold temperature difference
• Darcy-Weisbach Pressure and Major Head Loss Equation - The Darcy-Weisbach equation can be used to calculate the major pressure or head loss due to friction in ducts, pipes or tubes
• Hydraulic Diameter - Hydraulic diameter of pipes and ducts
• Minor or Dynamic Loss Coefficients for Pipe or Tube System Components - Minor loss coefficients for commonly used components in pipe and tube systems
• Pressure Gradient Diagrams - A pressure gradient diagram is a graphical presentation of the static pressure throughout a fluid flow system
• PVC - Friction Loss in Fittings and Equivalent Length - Minor loss in PVC and CPVC fittings as equivalent length of straight pipe
• Total Head Loss in Pipe or Duct Systems - Major and minor loss in pipe, tubes and duct systems
• Water Flow and Velocity Head in Steel Pipes - Schedule 40 - Velocity head used to calculate minor pressure or head loss in fluid flow systems

Ploss Valve

Tag Search

Ploss Valve Pic

• en: minor loss pipe tube duct system
• es: sistema de conductos de tubo tubo de pérdida menor
• de: geringen Verlust Rohr Rohrleitungssystem